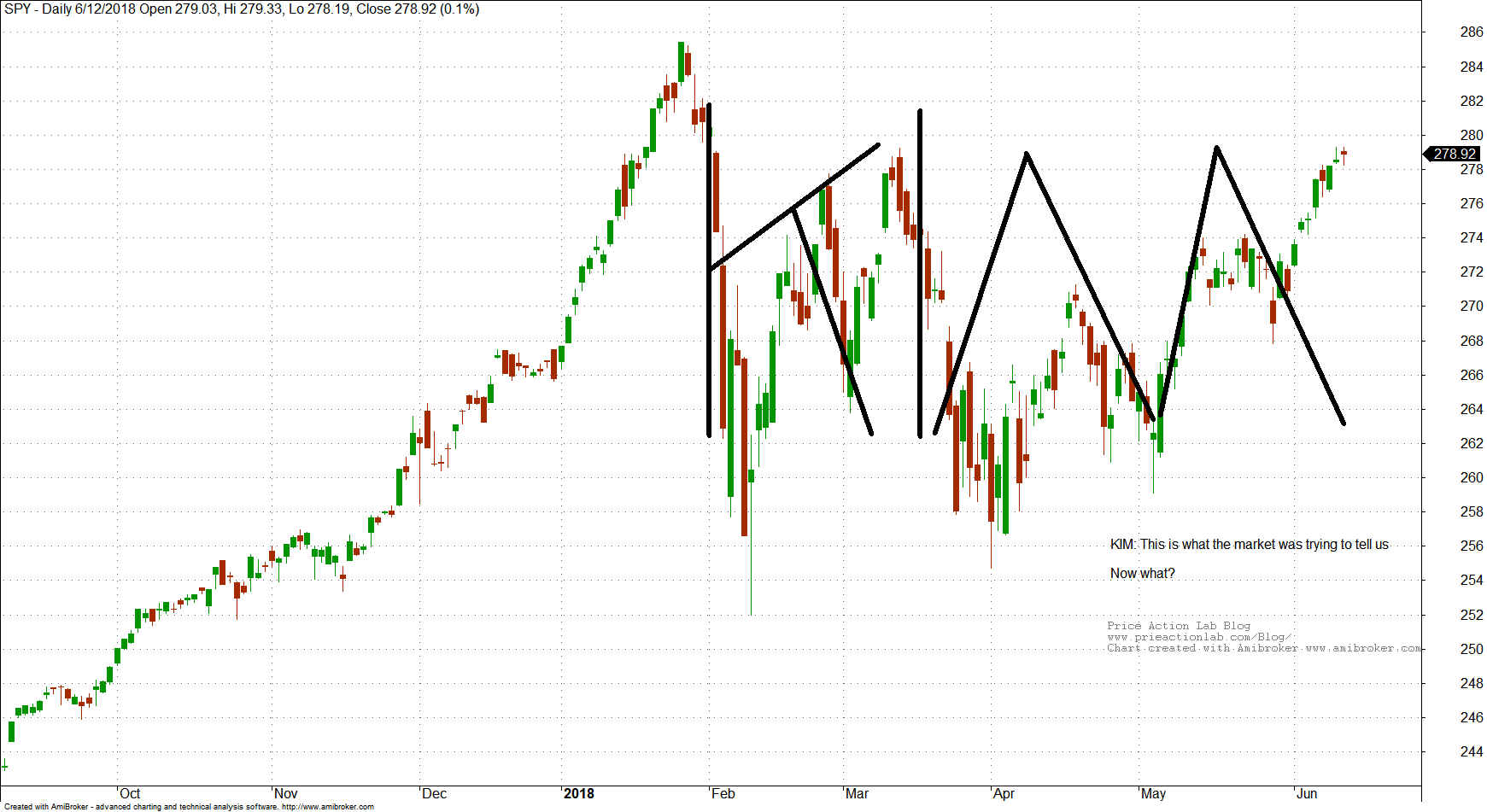
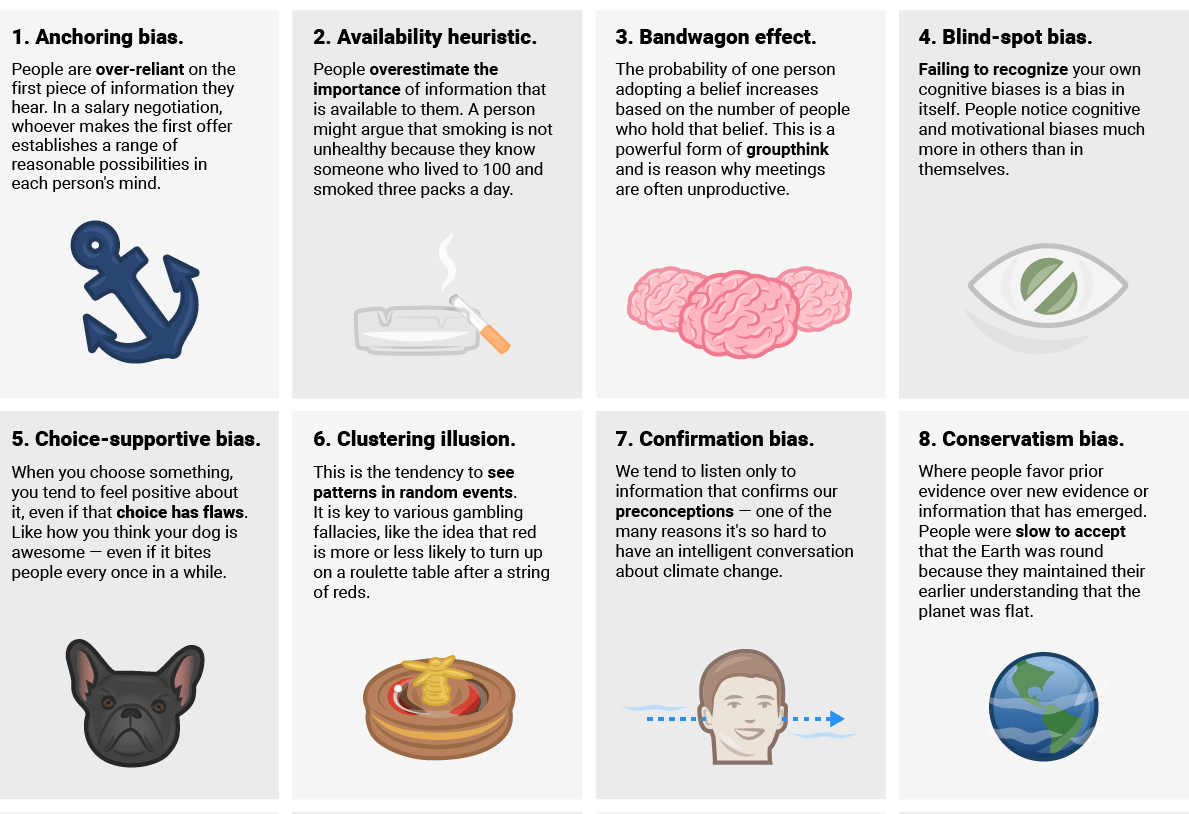
Clustering Illusion Bias. The tendency to see patterns in random events. It is key to various gambling. Join My FREE Coaching Program - 🔥 PRODUCTIVITY MASTERMIND 🔥Link - 👈 Inside the Program: 👉 WEEKLY LIVE. Many people would conclude Tom is 'lucky'. In this example we had a group or cluster of four coin tosses that led to an unexpected result. The 'surprising' result is called The Clustering Illusion. Tom's ability to get four heads in a row led some to suspect he was lucky, has. The 'Illusion of Asymmetric Insight' occurs where we believe we understand others better than they understand themselves. This is what the clustering illusion is—seeing significant patterns or clumps in data that are really random. Another example of the clustering illusion occurred during World War II, when the Germans bombed South London. Some areas were hit several times and others not at all.

1. Clustering Illusion Examples
2. Business Clustering Examples
3. Random Illusions
4. Data Clustering Example

The clustering illusion is the tendency to erroneously consider the inevitable 'streaks' or 'clusters' arising in small samples from random distributions to be non-random. The illusion is caused by a human tendency to underpredict the amount of variability likely to appear in a small sample of random or semi-random data.^[1]

Contents

Examples

Thomas Gilovich, an early author on the subject, argued that the effect occurs for different types of random dispersions, including two-dimensional data such as clusters in the locations of impact of World War IIV-1 flying bombs on maps of London; or seeing patterns in stock market price fluctuations over time.^[1][2] Although Londoners developed specific theories about the pattern of impacts within London, a statistical analysis by R. D. Clarke originally published in 1946 showed that the impacts of V-2 rockets on London were a close fit to a random distribution.^{[3][4][5][6][7]}

Similar biases

Using this cognitive bias in causal reasoning may result in the Texas sharpshooter fallacy. More general forms of erroneous pattern recognition are pareidolia and apophenia. Related biases are the illusion of control which the clustering illusion could contribute to, and insensitivity to sample size in which people don't expect greater variation in smaller samples. A different cognitive bias involving misunderstanding of chance streams is the gambler's fallacy.

Possible causes

Daniel Kahneman and Amos Tversky explained this kind of misprediction as being caused by the representativeness heuristic^[2] (which itself they also first proposed).

See also

Related Research Articles

The gambler's fallacy, also known as the Monte Carlo fallacy or the fallacy of the maturity of chances, is the erroneous belief that if a particular event occurs more frequently than normal during the past it is less likely to happen in the future, when it has otherwise been established that the probability of such events does not depend on what has happened in the past. Such events, having the quality of historical independence, are referred to as statistically independent. The fallacy is commonly associated with gambling, where it may be believed, for example, that the next dice roll is more than usually likely to be six because there have recently been less than the usual number of sixes.

A cognitive bias is a systematic pattern of deviation from norm or rationality in judgment. Individuals create their own 'subjective reality' from their perception of the input. An individual's construction of reality, not the objective input, may dictate their behavior in the world. Thus, cognitive biases may sometimes lead to perceptual distortion, inaccurate judgment, illogical interpretation, or what is broadly called irrationality.

Clustering Illusion Examples

Daniel Kahneman is an Israeli psychologist and economist notable for his work on the psychology of judgment and decision-making, as well as behavioral economics, for which he was awarded the 2002 Nobel Memorial Prize in Economic Sciences. His empirical findings challenge the assumption of human rationality prevailing in modern economic theory.

Amos Nathan Tversky was an Israeli cognitive and mathematical psychologist, a student of cognitive science, a collaborator of Daniel Kahneman, and a key figure in the discovery of systematic human cognitive bias and handling of risk.

The Texas sharpshooter fallacy is an informal fallacy which is committed when differences in data are ignored, but similarities are overemphasized. From this reasoning, a false conclusion is inferred. This fallacy is the philosophical or rhetorical application of the multiple comparisons problem and apophenia. It is related to the clustering illusion, which is the tendency in human cognition to interpret patterns where none actually exist.

The representativeness heuristic is used when making judgments about the probability of an event under uncertainty. It is one of a group of heuristics proposed by psychologists Amos Tversky and Daniel Kahneman in the early 1970s as 'the degree to which [an event] (i) is similar in essential characteristics to its parent population, and (ii) reflects the salient features of the process by which it is generated'. Heuristics are described as 'judgmental shortcuts that generally get us where we need to go – and quickly – but at the cost of occasionally sending us off course.' Heuristics are useful because they use effort-reduction and simplification in decision-making.

The conjunction fallacy is a formal fallacy that occurs when it is assumed that specific conditions are more probable than a single general one.

Thomas Dashiff Gilovich is the Irene Blecker Rosenfeld Professor of Psychology at Cornell University. He has conducted research in social psychology, decision making, behavioral economics, and has written popular books on these subjects. Gilovich has collaborated with Daniel Kahneman, Richard Nisbett, Lee Ross and Amos Tversky. His articles in peer-reviewed journals on subjects such as cognitive biases have been widely cited. In addition, Gilovich has been quoted in the media on subjects ranging from the effect of purchases on happiness to perception of judgment in social situations. Gilovich is a fellow of the Committee for Skeptical Inquiry.

The planning fallacy is a phenomenon in which predictions about how much time will be needed to complete a future task display an optimism bias and underestimate the time needed. This phenomenon sometimes occurs regardless of the individual's knowledge that past tasks of a similar nature have taken longer to complete than generally planned. The bias affects predictions only about one's own tasks; when outside observers predict task completion times, they show a pessimistic bias, overestimating the time needed. The planning fallacy requires that predictions of current tasks' completion times are more optimistic than the beliefs about past completion times for similar projects and that predictions of the current tasks' completion times are more optimistic than the actual time needed to complete the tasks.

Apophenia is the tendency to perceive meaningful connections between seemingly unrelated things. The term was coined by psychiatrist Klaus Conrad in his 1958 publication on the beginning stages of schizophrenia. He defined it as 'unmotivated seeing of connections [accompanied by] a specific feeling of abnormal meaningfulness'. He described the early stages of delusional thought as self-referential, over-interpretations of actual sensory perceptions, as opposed to hallucinations.

The overconfidence effect is a well-established bias in which a person's subjective confidence in his or her judgments is reliably greater than the objective accuracy of those judgments, especially when confidence is relatively high. Overconfidence is one example of a miscalibration of subjective probabilities. Throughout the research literature, overconfidence has been defined in three distinct ways: (1) overestimation of one's actual performance; (2) overplacement of one's performance relative to others; and (3) overprecision in expressing unwarranted certainty in the accuracy of one's beliefs.

The 'hot hand' was considered a cognitive social bias that a person who experiences a successful outcome has a greater chance of success in further attempts. The concept is often applied to sports and skill-based tasks in general and originates from basketball, where a shooter is allegedly more likely to score if their previous attempts were successful, i.e. while having 'hot hands.” While previous success at a task can indeed change the psychological attitude and subsequent success rate of a player, researchers for many years did not find evidence for a 'hot hand' in practice, dismissing it as fallacious. However, later research questioned whether the belief is indeed a fallacy. Recent studies using modern statistical analysis show there is evidence for the 'hot hand' in some sporting activities.

Heuristics are simple strategies or mental processes that humans, animals, organizations and machines use to quickly form judgments, make decisions, and find solutions to complex problems. This happens when an individual focuses on the most relevant aspects of a problem or situation to formulate a solution.

Thinking, Fast and Slow is a best-selling book published in 2011 by Nobel Memorial Prize in Economic Sciences laureate Daniel Kahneman. It was the 2012 winner of the National Academies Communication Award for best creative work that helps the public understanding of topics in behavioral science, engineering and medicine.

Insensitivity to sample size is a cognitive bias that occurs when people judge the probability of obtaining a sample statistic without respect to the sample size. For example, in one study subjects assigned the same probability to the likelihood of obtaining a mean height of above six feet [183 cm] in samples of 10, 100, and 1,000 men. In other words, variation is more likely in smaller samples, but people may not expect this.

Extension neglect is a type of cognitive bias which occurs when the sample size is ignored while evaluating a study in which the sample size is logically relevant. For instance, when reading an article about a scientific study, extension neglect occurs when the reader ignores the number of people involved in the study but still makes inferences about a population based on the sample. In reality, if the sample size is too small, the results might risk errors in statistical hypothesis testing. A study based on only a few people may draw invalid conclusions because only one person has exceptionally high or low scores (outlier), and there are not enough people there to correct this via averaging out. But often, the sample size is not prominently displayed in science articles, and the reader in this case might still believe the article's conclusion due to extension neglect.

Illusion of validity is a cognitive bias in which a person overestimates his or her ability to interpret and predict accurately the outcome when analyzing a set of data, in particular when the data analyzed show a very consistent pattern—that is, when the data 'tell' a coherent story.

In cognitive psychology and decision science, conservatism or conservatism bias is a bias which refers to the tendency to revise one's belief insufficiently when presented with new evidence. This bias describes human belief revision in which people over-weigh the prior distribution and under-weigh new sample evidence when compared to Bayesian belief-revision.

Business Clustering Examples

Intuitive statistics, or folk statistics, refers to the cognitive phenomenon where organisms use data to make generalizations and predictions about the world. This can be a small amount of sample data or training instances, which in turn contribute to inductive inferences about either population-level properties, future data, or both. Inferences can involve revising hypotheses, or beliefs, in light of probabilistic data that inform and motivate future predictions. The informal tendency for cognitive animals to intuitively generate statistical inferences, when formalized with certain axioms of probability theory, constitutes statistics as an academic discipline.

References

1. Gilovich, Thomas (1991). How we know what isn't so: The fallibility of human reason in everyday life. New York: The Free Press. ISBN978-0-02-911706-4.
2. Kahneman, Daniel; Amos Tversky (1972). 'Subjective probability: A judgment of representativeness'. Cognitive Psychology. 3 (3): 430–454. doi:10.1016/0010-0285(72)90016-3.
3. ↑ Clarke, R. D. (1946). 'An application of the Poisson distribution'. Journal of the Institute of Actuaries. 72 (3): 481. doi:10.1017/S0020268100035435.
4. ↑ Gilovich, 1991 p. 19
5. ↑ Mori, Kentaro. 'Seeing patterns'. Retrieved 3 March 2012.
6. ↑ 'Bombing London'. Archived from the original on 2012-02-21. Retrieved 3 March 2012.
7. ↑ Tierney, John (3 October 2008). 'See a pattern on Wall Street?'(October 3, 2008). TierneyLab. New York Times. Retrieved 3 March 2012.

External links

Random Illusions

The clustering illusion is the human tendency to expect random events to appear more regular or uniform than they are in reality, resulting in the assumption that clusters in the data cannot be caused by chance alone. An important example of this is that the stars in the night sky seem clumped together in some regions, while there are “empty” spots in other regions. The clustering illusion is then simply the tendency to expect that there must be some sort of physical explanation for this (e.g., the stars must be physically grouped in space), since it “doesn’t seem truly random”. In reality, however, the position of the stars is random, and it is our expectation of the variability that is wrong. The image on the left below shows an example of a truly random star field. The image on the right is a random star field that is too uniform to be realistic, but that might be closer to what a human would draw if you would ask him or her to create such a star field manually. In the example on the right, each single star is placed randomly in its own 20 × 20 pixel square, producing a more uniform, but unrealistic, effect.

Simulated Geiger Counter

A second example is radioactive decay, which is really the quintessential example of randomness, since each decay is an independent event that is not influenced by earlier decays, and that is unpredictable on a very fundamental (quantum mechanical) level. Clicking the Start simulation button below starts a simulated Geiger counter, which produces an audible “tick” for each simulated decay event. The simulated decay rate is two events per second. The groups of events that seem to be present, have no physical meaning.

counts: 0

I am aware that a browser with JavaScript is not ideal for this kind of time-related work, but it is good enough for this demonstration. It does not work very well anymore if you switch to another tab, since the JavaScript in a background tab is given lower priority. In Simulating a Geiger Counter, I explain how this simulation works.

Data Clustering Example

Add new comment